Algorithms in Data Structure
Data Structure and Algorithms is an essential thing to build a scalable application. Data Structure is a way of collecting and organizing data in such a manner that we can perform operations on these data easily and effectively while an algorithm is a finite set of sequential instructions to accomplish a certain predefined task. Steps of an algorithm may have branching or repetition depending upon the problem for which the algorithm has been developed. An algorithm is written in human understandable language. It is independent of any programming language. We can implement an algorithm in any programming language according to our convenience. An algorithm is not the complete code but the core logic to resolve the problem in step-by-step manner.
Properties of a good algorithm
An algorithm is language independent and always written in simple language so that anyone can easily understand it. A good algorithm has following features:
- A good algorithm must always terminate after a finite number of steps.
- Each step of an algorithm must be precisely defined. The actions to be carried out must be clearly specified for each case.
- An algorithm has zero or more inputs.
- An algorithm has one or more outputs.
- An algorithm is expected to be effective. All of the operations to be performed in the algorithm must be easily understandable and must be completed in a finite length of time.
In practice, length of time taken to perform the algorithm, adaptability of the algorithm to computers, its simplicity and elegance, etc. are the basic criterion on the basis of which we can decide whether an algorithm is good or not.
Efficiency of an algorithm depends on the time taken to execute it and the memory it consumes for its execution. The performance of an algorithm is measured on the basis of:
Time Complexity: a way to represent the amount of time required by the program to run till its completion.
Space Complexity: the amount of memory space required by the algorithm, during the course of its execution.
How to write an algorithm?
As we know it is language independent, there is no hard and fast rule or standard to write an algorithm. It is dependent on problem and resources we have. We can simply use common constructs like loops (while, do-while, for) and conditional statements (if-else) for writing because these are common to all programming languages. We write algorithms in a step-by-step manner, but it is not always the case. Algorithm writing is a process and is executed after the problem domain is well-defined. That is, we should know the problem domain, for which we are designing a solution.
Example
Let us take an example to check whether a number entered by user is prime or not.
Step 1: Start Step 2: Declare variables n,i,flag. Step 3: Initialize variables flag←1 i←2 Step 4: Read n from user. Step 5: Repeat the steps until i<(n/2) 5.1 If remainder of n÷i equals 0 flag←0 Go to step 6 5.2 i←i+1 Step 6: If flag=0 Display n is not prime else Display n is prime Step 7: Stop
Algorithm is not the computer code or programming language. It’s just the step-by-step instructions which gives clear idea about writing the computer code in your convenient programming language.
Asymptotic Notation
Asymptotic notations are some standard notation that we use to analyze the complexity of any algorithm in terms of time and space.
When we analyze an algorithm, we generally represent the amount of time required for execution or the time required by the computer to run the lines of code of the algorithm, number of memory accesses, number of comparisons, temporary variables occupying memory space etc. using formula that often contains unimportant details and don’t tell us anything about the running time actually.
Asymptotic notations that we commonly used to calculate the running time complexity of an algorithm.
- Ο Notation
- Ω Notation
- θ Notation
Big O Notation
Big O notation is known as the upper bound of the algorithm. It is Worst Case of an algorithm. It tells a certain function will never exceed a specified time for any value of input n. It measures the worst case time complexity or the longest amount of time an algorithm can possibly take to complete.
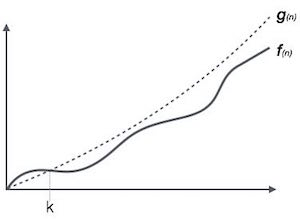
For example, let us assume Linear Search algorithm in which we traverse an array elements one by one to search a number.
In Worst case, starting from the front of the array, we find the element we are looking for at the end. That leads to a time complexity of n, where n represents the number of total elements. But it can happen that the element that we are searching is the first element of the array, in this case the time complexity will be 1. Now in this case, saying that the big-Θ time complexity for Linear search is Θ(n) that means the time required will always be related to n, as this is the right way to represent the average time complexity, but when we use the big-O notation, we mean to say that the time complexity is O(n), which means that the time complexity will never exceed n, hence saying that it can be less than or equal to n, which is the correct representation. This is the reason, most of the time you will see Big-O notation being used to represent the time complexity of any algorithm, because it makes more sense.
For a function f(n)
Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that f(n) ≤ c.g(n) for all n > n0. }
Omega Notation, Ω
Omega notation is used to define the lower bound of any algorithm. It represents the best case of any algorithm because it always indicates the minimum time required for any algorithm for all input values.
When we represent a time complexity for any algorithm in the form of Ω, we mean that the algorithm will take at least this much time to complete its execution.
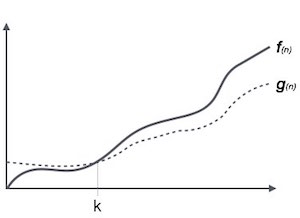
For a function f(n)
Ω(f(n)) ≥ { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }
Theta Notation, θ
The time complexity represented by θ notation is like the average value. It represents a range within which the actual time of execution of the algorithm will lie.
For example, if for some algorithm the time complexity is represented by the expression 3n2 + 5n, and we use θ notation to represent this, then the time complexity would be θ (n2), ignoring the constant coefficient and removing the insignificant part, which is 5n. Here, complexity of θ (n2) means, the average time for any input n will remain in between, k1 * n2 and k2 * n2, where k1, k2 are two constants.
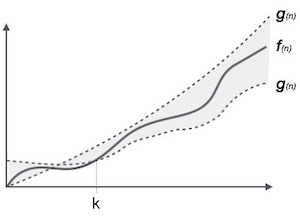
For a function f(n)
θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }
Space Complexity of an Algorithm
Space complexity is the amount of memory used by algorithms to execute and produce the result. It also include input values and the auxiliary spaces.
Memory is used for 3 different purposes at the time of executing algorithms:
Instruction Space: memory used to save the compiled version of instructions.
Environmental Stack: Sometimes an algorithm may be called inside another. In such a situation, current variables are pushed onto the system stack, where they wait for further execution and then the call to the inside algorithm is made.
Data Space: Amount of space used by the variables and constants.
But, at the time of Space Complexity calculation of any algorithm, we usually consider Data Space only. Instruction Space and Environmental Stack are usually neglected.
Time Complexity of an Algorithm
Time complexity of an algorithm signifies the total time required by the program to run till its completion. It is most commonly expressed using the big O notation. Time Complexity is most commonly estimated by counting the number of elementary steps performed by any algorithm to finish execution.
Algorithm’s performance may vary with different types of input data, hence for algorithms we usually use the worst-case Time complexity because that is the maximum time taken.
Types of Notations for Time Complexity:
Big O denotes “fewer than or the same as” <expression> iterations.
Big Ω denotes “more than or the same as” <expression> iterations.
Big θ denotes “the same as” <expression> iterations.
Little O denotes “fewer than” <expression> iterations.
Little Ω denotes “more than” <expression> iterations.
Categories of algorithms
From the data structure point of view, following are some important categories of algorithms:
Search: to search an item in a data structure.
Sort: to sort items in a certain order.
Insert: to insert item in a data structure.
Update: to update an existing item in a data structure.
Delete: to delete an existing item from a data structure.
Was this article helpful? Must share your views in the comment section below. Keep visiting our Tech Blogs to stay updated with our future posts.

